[TOC]

0. Transformer直观认识

Transformer 和 LSTM 的最大区别，就是 LSTM 的训练是迭代的、串行的，必须要等当前字处理完，才可以处理下一个字。而 Transformer 的训练时并行的，即所有字是同时训练的，这样就大大增加了计算效率。Transformer 使用了位置嵌入 (Positional Encoding) 来理解语言的顺序，使用自注意力机制（Self Attention Mechanism）和全连接层进行计算。

Transformer 模型主要分为两大部分，分别是 Encoder 和 Decoder。Encoder 负责把输入（语言序列）隐射成隐藏层，然后解码器再把隐藏层映射为自然语言序列。

encoder

上图为 Transformer Encoder Block 结构图，注意：下面的内容标题编号分别对应着图中 1,2,3,4 个方框的序号

1. Positional Encoding

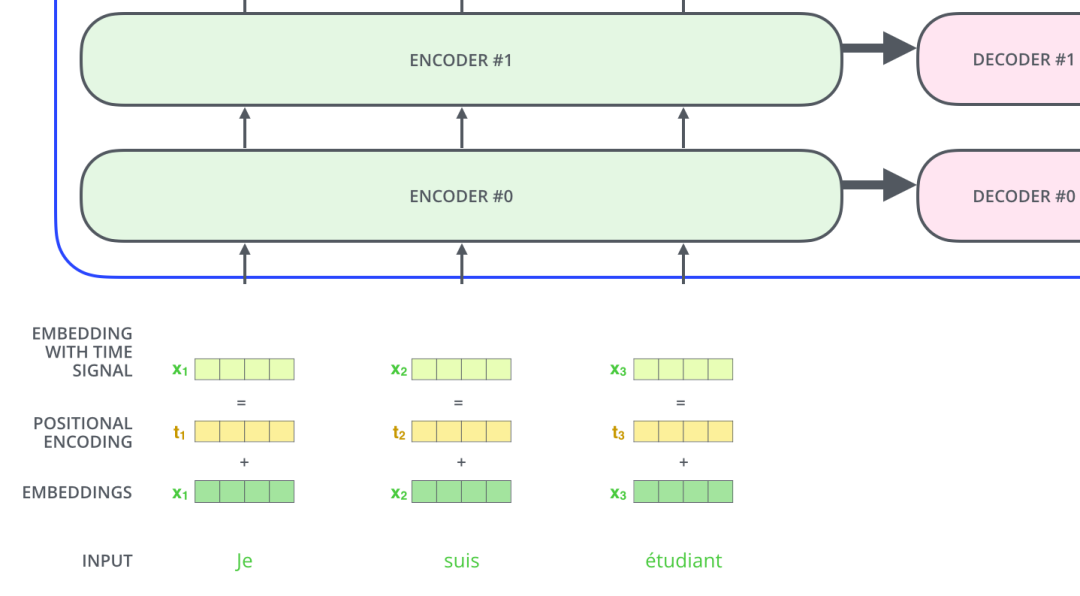
如下图所示，Transformer模型对每个输入的词向量都加上了一个位置向量。这些向量有助于确定每个单词的位置特征，或者句子中不同单词之间的距离特征。词向量加上位置向量背后的直觉是：将这些表示位置的向量添加到词向量中，得到的新向量，可以为模型提供更多有意义的信息，比如词的位置，词之间的距离等。

位置向量

现在定义一个位置嵌入的概念，也就是 Positional Encoding，位置嵌入的维度为 [max_sequence_length, embedding_dimension], 位置嵌入的维度与词向量的维度是相同的，都是 embedding_dimension。max_sequence_length 属于超参数，指的是限定每个句子最长由多少个词构成。

我们一般以字为单位训练 Transformer 模型。首先初始化字编码的大小为 [vocab_size, embedding_dimension]，vocab_size 为字库中所有字的数量，embedding_dimension 为字向量的维度，对应到 PyTorch 中，其实就是 nn.Embedding(vocab_size, embedding_dimension)。

原始论文中给出的位置编码信息的向量的设计表达式为：

$PE(pos,2i)=sin(pos/10000^{2i/d_{model}})\\ PE(pos,2i+1)=cos(pos/10000^{2i/d_{model}})$

上面表达式中的$pos$代表词的位置,取值范围是[0,max_sequence_length]，$d_{model}$代表位置向量的维度，i 代表位置$d_{model}$维位置向量第i维,指字向量的维度序号，取值范围[0,embedding_dimension/2]。

上面有 sin 和 cos 一组公式，也就是对应着 embedding_dimension 维度的一组奇数和偶数的序号的维度，分别用上面的 sin 和 cos 函数做处理，从而产生不同的周期性变化，而位置嵌入在 embedding_dimension维度上随着维度序号增大，周期变化会越来越慢，最终产生一种包含位置信息的纹理，就像论文原文中第六页讲的，位置嵌入函数的周期从 2π 到 10000∗2π 变化，而每一个位置在 embedding_dimension维度上都会得到不同周期的 sin 和 cos 函数的取值组合，从而产生独一的纹理位置信息，最终使得模型学到位置之间的依赖关系和自然语言的时序特性。

在下图中，我们画出了一种位置向量在第4、5、6、7维度、不同位置的的数值大小。横坐标表示位置下标，纵坐标表示数值大小。

位置编码

如果不理解这里为何这么设计，可以看这篇文章 Transformer 中的 Positional Encoding

2. Self Attention Mechanism

对于输入的句子$ X $，通过 WordEmbedding 得到该句子中每个字的字向量，同时通过 Positional Encoding 得到所有字的位置向量，将其相加（维度相同，可以直接相加），得到该字真正的向量表示。第 $t $个字的向量记作$ x_t $。

先通过一个简单的例子来理解一下：什么是“self-attention自注意力机制”？假设一句话包含两个单词：Thinking Machines。自注意力的一种理解是：Thinking-Thinking，Thinking-Machines，Machines-Thinking，Machines-Machines，共$2^2$种两两attention。那么具体如何计算呢？假设Thinking、Machines这两个单词经过词向量算法得到向量是$X_1$,$ X_2$：

下面，我们将self-attention计算的6个步骤进行可视化。

第1步：对输入编码器的词向量进行线性变换得到：Query向量: $q_1,q_2$，Key向量: $k_1, k_2$，Value向量: $v_1, v_2$。这3个向量是词向量分别和3个参数矩阵相乘得到的，而这个矩阵也是是模型要学习的参数。attention计算的逻辑常常可以描述为：query和key计算相关或者叫attention得分，然后根据attention得分对value进行加权求和。

qkv

第2步：计算Attention Score（注意力分数）。假设我们现在计算第一个词Thinking 的Attention Score（注意力分数），需要根据Thinking 对应的词向量，对句子中的其他词向量都计算一个分数。这些分数决定了我们在编码Thinking这个词时，需要对句子中其他位置的词向量的权重。

Attention score是根据”Thinking“ 对应的 Query 向量和其他位置的每个词的 Key 向量进行点积得到的。Thinking的第一个Attention Score就是$q_1$和$k_1$的内积，第二个分数就是$q_1$和$k_2$的点积。这个计算过程在下图中进行了展示，下图里的具体得分数据是为了表达方便而自定义的。

think

第3步：把每个分数除以 $\sqrt{d_k}，d_{k}$是Key向量的维度。你也可以除以其他数，除以一个数是为了在反向传播时，求梯度时更加稳定。

第4步：接着把这些分数经过一个Softmax函数，Softmax可以将分数归一化，这样使得分数都是正数并且加起来等于1，如下图所示。这些分数决定了Thinking词向量，对其他所有位置的词向量分别有多少的注意力。

think2

第5步：得到每个词向量的分数后，将分数分别与对应的Value向量相乘。这种做法背后的直觉理解就是：对于分数高的位置，相乘后的值就越大，我们把更多的注意力放到了它们身上；对于分数低的位置，相乘后的值就越小，这些位置的词可能是相关性不大的。

第6步：把第5步得到的Value向量相加，就得到了Self Attention在当前位置（这里的例子是第1个位置）对应的输出。

最后，在下图展示了对第一个位置词向量计算Self Attention 的全过程。最终得到的当前位置（这里的例子是第一个位置）词向量会继续输入到前馈神经网络。注意：上面的6个步骤每次只能计算一个位置的输出向量，在实际的代码实现中，Self Attention的计算过程是使用矩阵快速计算的，一次就得到所有位置的输出向量。

sum

self-attention矩阵运算

将self-attention计算6个步骤中的向量放一起，比如X=[x_1;x_2]X=[x1;x2]，便可以进行矩阵计算啦。下面，依旧按步骤展示self-attention的矩阵计算方法。

$X=[X1;X2]\\Q=XW^Q,K=XW^K,V=XW^V\\Z=softmax(\frac {QK^T}{\sqrt(d_k)})V$

第1步：计算 Query，Key，Value 的矩阵。首先，我们把所有词向量放到一个矩阵X中，然后分别和3个权重矩阵$W^Q,W^K,W^V$相乘，得到 Q，K，V 矩阵。矩阵X中的每一行，表示句子中的每一个词的词向量。Q，K，V 矩阵中的每一行表示 Query向量，Key向量，Value 向量，向量维度是$d_k$。

第2步：由于我们使用了矩阵来计算，我们可以把上面的第 2 步到第 6 步压缩为一步，直接得到 Self Attention 的输出。

Multi-Head Attention（多头注意力机制）

Transformer 的论文通过增加多头注意力机制（一组注意力称为一个 attention head），进一步完善了Self-Attention。这种机制从如下两个方面增强了attention层的能力：

它扩展了模型关注不同位置的能力。在上面的例子中，第一个位置的输出z_1z1包含了句子中其他每个位置的很小一部分信息，但z_1z1仅仅是单个向量，所以可能仅由第1个位置的信息主导了。而当我们翻译句子：The animal didn’t cross the street because it was too tired时，我们不仅希望模型关注到”it”本身，还希望模型关注到”The”和“animal”，甚至关注到”tired”。这时，多头注意力机制会有帮助。
多头注意力机制赋予attention层多个“子表示空间”。下面我们会看到，多头注意力机制会有多组$W^Q, W^K,W^V$ 的权重矩阵（在 Transformer 的论文中，使用了 8 组注意力),因此可以将$X$变换到更多种子空间进行表示。接下来我们也使用8组注意力头（attention heads））。每一组注意力的权重矩阵都是随机初始化的，但经过训练之后，每一组注意力的权重$W^Q,W^K,W^V$ 可以把输入的向量映射到一个对应的”子表示空间“。

多头注意力机制

在多头注意力机制中，我们为每组注意力设定单独的 WQ, WK, WV 参数矩阵。将输入X和每组注意力的WQ, WK, WV 相乘，得到8组 Q, K, V 矩阵。

接着，我们把每组 K, Q, V 计算得到每组的 Z 矩阵，就得到8个Z矩阵。

由于前馈神经网络层接收的是 1 个矩阵（其中每行的向量表示一个词），而不是 8 个矩阵，所以我们直接把8个子矩阵拼接起来得到一个大的矩阵，然后和另一个权重矩阵$W^O$相乘做一次变换，映射到前馈神经网络层所需要的维度。

以上就是多头注意力的全部内容。最后将所有内容放到一张图中：

总的多头

Attention代码

下面的代码实现中，张量的第1维是 batch size，第 2 维是句子长度。代码中进行了详细注释和说明。

class MultiheadAttention(nn.Module):
    # n_heads：多头注意力的数量
    # hid_dim：每个词输出的向量维度
    def __init__(self, hid_dim, n_heads, dropout):
        super(MultiheadAttention, self).__init__()
        self.hid_dim = hid_dim
        self.n_heads = n_heads

        # 强制 hid_dim 必须整除 h
        assert hid_dim % n_heads == 0
        # 定义 W_q 矩阵
        self.w_q = nn.Linear(hid_dim, hid_dim)
        # 定义 W_k 矩阵
        self.w_k = nn.Linear(hid_dim, hid_dim)
        # 定义 W_v 矩阵
        self.w_v = nn.Linear(hid_dim, hid_dim)
        self.fc = nn.Linear(hid_dim, hid_dim)
        self.do = nn.Dropout(dropout)
        # 缩放
        self.scale = torch.sqrt(torch.FloatTensor([hid_dim // n_heads]))

    def forward(self, query, key, value, mask=None):
        # 注意 Q，K，V的在句子长度这一个维度的数值可以一样，可以不一样。
        # K: [64,10,300], 假设batch_size 为 64，有 10 个词，每个词的 Query 向量是 300 维
        # V: [64,10,300], 假设batch_size 为 64，有 10 个词，每个词的 Query 向量是 300 维
        # Q: [64,12,300], 假设batch_size 为 64，有 12 个词，每个词的 Query 向量是 300 维
        bsz = query.shape[0]
        Q = self.w_q(query)
        K = self.w_k(key)
        V = self.w_v(value)
        # 这里把 K Q V 矩阵拆分为多组注意力
        # 最后一维就是是用 self.hid_dim // self.n_heads 来得到的，表示每组注意力的向量长度, 每个 head 的向量长度是：300/6=50
        # 64 表示 batch size，6 表示有 6组注意力，10 表示有 10 词，50 表示每组注意力的词的向量长度
        # K: [64,10,300] 拆分多组注意力 -> [64,10,6,50] 转置得到 -> [64,6,10,50]
        # V: [64,10,300] 拆分多组注意力 -> [64,10,6,50] 转置得到 -> [64,6,10,50]
        # Q: [64,12,300] 拆分多组注意力 -> [64,12,6,50] 转置得到 -> [64,6,12,50]
        # 转置是为了把注意力的数量 6 放到前面，把 10 和 50 放到后面，方便下面计算
        Q = Q.view(bsz, -1, self.n_heads, self.hid_dim //
                   self.n_heads).permute(0, 2, 1, 3)
        K = K.view(bsz, -1, self.n_heads, self.hid_dim //
                   self.n_heads).permute(0, 2, 1, 3)
        V = V.view(bsz, -1, self.n_heads, self.hid_dim //
                   self.n_heads).permute(0, 2, 1, 3)

        # 第 1 步：Q 乘以 K的转置，除以scale
        # [64,6,12,50] * [64,6,50,10] = [64,6,12,10]
        # attention：[64,6,12,10]
        attention = torch.matmul(Q, K.permute(0, 1, 3, 2)) / self.scale

        # 如果 mask 不为空，那么就把 mask 为 0 的位置的 attention 分数设置为 -1e10，这里用“0”来指示哪些位置的词向量不能被attention到，比如padding位置，当然也可以用“1”或者其他数字来指示，主要设计下面2行代码的改动。
        if mask is not None:
            attention = attention.masked_fill(mask == 0, -1e10)

        # 第 2 步：计算上一步结果的 softmax，再经过 dropout，得到 attention。
        # 注意，这里是对最后一维做 softmax，也就是在输入序列的维度做 softmax
        # attention: [64,6,12,10]
        attention = self.do(torch.softmax(attention, dim=-1))

        # 第三步，attention结果与V相乘，得到多头注意力的结果
        # [64,6,12,10] * [64,6,10,50] = [64,6,12,50]
        # x: [64,6,12,50]
        x = torch.matmul(attention, V)

        # 因为 query 有 12 个词，所以把 12 放到前面，把 50 和 6 放到后面，方便下面拼接多组的结果
        # x: [64,6,12,50] 转置-> [64,12,6,50]
        x = x.permute(0, 2, 1, 3).contiguous()
        # 这里的矩阵转换就是：把多组注意力的结果拼接起来
        # 最终结果就是 [64,12,300]
        # x: [64,12,6,50] -> [64,12,300]
        x = x.view(bsz, -1, self.n_heads * (self.hid_dim // self.n_heads))
        x = self.fc(x)
        return x


# batch_size 为 64，有 12 个词，每个词的 Query 向量是 300 维
query = torch.rand(64, 12, 300)
# batch_size 为 64，有 12 个词，每个词的 Key 向量是 300 维
key = torch.rand(64, 10, 300)
# batch_size 为 64，有 10 个词，每个词的 Value 向量是 300 维
value = torch.rand(64, 10, 300)
attention = MultiheadAttention(hid_dim=300, n_heads=6, dropout=0.1)
output = attention(query, key, value)
## output: torch.Size([64, 12, 300])
print(output.shape)

Padding Mask

pad

上面 Self Attention 的计算过程中，我们通常使用 mini-batch 来计算，也就是一次计算多句话，即 $X$ 的维度是 [batch_size, sequence_length]，sequence_length是句长，而一个 mini-batch 是由多个不等长的句子组成的，我们需要按照这个 mini-batch 中最大的句长对剩余的句子进行补齐，一般用 0 进行填充，这个过程叫做 padding。

但这时在进行 softmax 就会产生问题。回顾 softmax 函数 $σ(z_i)=\frac {e^{z_i}}{∑_{j=1}^Ke^z_j}$，$e^0$ 是 1，是有值的，这样的话 softmax 中被 padding 的部分就参与了运算，相当于让无效的部分参与了运算，这可能会产生很大的隐患。因此需要做一个 mask 操作，让这些无效的区域不参与运算，一般是给无效区域加一个很大的负数偏置，即

$Z_{illegal}=Z_{illegal}+bias_{illegal}\\bias_{illegal}→−∞$

3.残差连接和Layer Normalization

到目前为止，我们计算得到了self-attention的输出向量。而单层encoder里后续还有两个重要的操作：残差连接、标准化。

编码器的每个子层（Self Attention 层和 FFNN）都有一个残差连接和层标准化（layer-normalization），如下图所示。

resnet

残差连接

我们在上一步得到了经过 self-attention 加权之后输出，也就是 Self-Attention(Q, K, V)，然后把他们加起来做残差连接。

$X_{embedding}+Self-Attention(Q, K, V)$

关于残差连接详细的解释可以看这篇文章【模型解读】resnet中的残差连接，你确定真的看懂了？ - 知乎 (zhihu.com)

Layer Normalization

Layer Normalization 的作用是把神经网络中隐藏层归一为标准正态分布，也就是 $i.i.d$ 独立同分布，以起到加快训练速度，加速收敛的作用。

$μ_j=\frac 1m∑_{i=1}^mx_{ij}$

上式以矩阵的列（column）为单位求均值；

$σ_j^2=\frac 1m∑_{i=1}^m(x_{ij}−μ_j)^2$

上式以矩阵的列（column）为单位求方差

$LayerNorm(x)=\frac {x_{ij}−μ_j}{\sqrt{σ_j^2+ϵ}}$

然后用每一列的每一个元素减去这列的均值，再除以这列的标准差，从而得到归一化后的数值，加 ϵ 是为了防止分母为 0。

层归一化

将 Self-Attention 层的层标准化（layer-normalization）和涉及的向量计算细节都进行可视化，如下所示：

标准化

编码器和和解码器的子层里面都有层标准化（layer-normalization）。假设一个 Transformer 是由 2 层编码器和两层解码器组成的，将全部内部细节展示起来如下图所示。

transformer示意图

4.Transformer Encoder整体架构

经过上面 3 个步骤，我们已经基本了解了 Encoder 的主要构成部分，下面我们用公式把一个 Encoder block 的计算过程整理一下：

1). 字向量与位置编码

$X=Embedding-Lookup(X)+Positional-Encoding$

2). 自注意力机制

$Q=Linear_q(X)=XW_Q\\K=Lineark(X)=XW_K\\V=Linearv(X)=XW_V\\X_{attention}=Self-Attention(Q,K,V)$

3). self-attention 残差连接与 Layer Normalization

$X_{attention}=X+X_{attention}\\X_{attention}=LayerNorm(X_{attention})$

4). 下面进行 Encoder block 结构图中的第 4 部分，也就是 FeedForward，其实就是两层线性映射并用激活函数激活，比如说 ReLU

$X_{hidden}=Linear(ReLU(Linear(X_{attention})))$

5). FeedForward 残差连接与 Layer Normalization

$X_{hidden}=X_{attention}+X_{hidden}\\X_{hidden}=LayerNorm(X_{hidden})$

其中

$X_{hidden}∈\mathbb{R}^{batch_size ∗ seq_len. ∗ embed_dim}$

5.Transformer Decoder整体架构

我们先从 HighLevel 的角度观察一下 Decoder 结构，从下到上依次是：

Masked Multi-Head Self-Attention
Multi-Head Encoder-Decoder Attention
FeedForward Network

和 Encoder 一样，上面三个部分的每一个部分，都有一个残差连接，后接一个 Layer Normalization。Decoder 的中间部件并不复杂，大部分在前面 Encoder 里我们已经介绍过了，但是 Decoder 由于其特殊的功能，因此在训练时会涉及到一些细节。

decoder

Masked Self-Attention

传统 Seq2Seq 中 Decoder 使用的是 RNN 模型，因此在训练过程中输入 $t$ 时刻的词，模型无论如何也看不到未来时刻的词，因为循环神经网络是时间驱动的，只有当 $t$ 时刻运算结束了，才能看到 t+1 时刻的词。而 Transformer Decoder 抛弃了 RNN，改为 Self-Attention，由此就产生了一个问题，在训练过程中，整个 ground truth 都暴露在 Decoder 中，这显然是不对的，我们需要对 Decoder 的输入进行一些处理，该处理被称为 Mask

举个例子，Decoder 的 ground truth 为 “ I am fine”，我们将这个句子输入到 Decoder 中，经过 WordEmbedding 和 Positional Encoding 之后，将得到的矩阵做三次线性变换（$W_Q,W_K,W_V$）。然后进行 self-attention 操作，首先通过 $\frac {Q×K^T}{\sqrt{d_k}}$ 得到 Scaled Scores，接下来非常关键，我们要对 Scaled Scores 进行 Mask，举个例子，当我们输入 “I” 时，模型目前仅知道包括 “I” 在内之前所有字的信息，即 ““ 和 “I” 的信息，不应该让其知道 “I” 之后词的信息。道理很简单，我们做预测的时候是按照顺序一个字一个字的预测，怎么能这个字都没预测完，就已经知道后面字的信息了呢？Mask 非常简单，首先生成一个下三角全 0，上三角全为负无穷的矩阵，然后将其与 Scaled Scores 相加即可。

之后再做 softmax，就能将 - inf 变为 0，得到的这个矩阵即为每个字之间的权重

Masked Encoder-Decoder Attention

其实这一部分的计算流程和前面 Masked Self-Attention 很相似，结构也一摸一样，唯一不同的是这里的 $K,V$ 为 Encoder 的输出，$Q$ 为 Decoder 中 Masked Self-Attention 的输出

编码器和解码器协同工作

编码器一般有多层，第一个编码器的输入是一个序列文本，最后一个编码器输出是一组序列向量，这组序列向量会作为解码器的$K、V$输入，其中K=V=解码器输出的序列向量表示。这些注意力向量将会输入到每个解码器的Encoder-Decoder Attention层，这有助于解码器把注意力集中到输入序列的合适位置，如下图所示。

解码（decoding ）阶段的每一个时间步都输出一个翻译后的单词（这里的例子是英语翻译），解码器当前时间步的输出又重新作为输入Q和编码器的输出K、V共同作为下一个时间步解码器的输入。然后重复这个过程，直到输出一个结束符。如下图所示：

decoder

解码器中的 Self Attention 层，和编码器中的 Self Attention 层的区别：

在解码器里，Self Attention 层只允许关注到输出序列中早于当前位置之前的单词。具体做法是：在 Self Attention 分数经过 Softmax 层之前，屏蔽当前位置之后的那些位置（将attention score设置成-inf）。
解码器 Attention层是使用前一层的输出来构造Query 矩阵，而Key矩阵和 Value矩阵来自于编码器最终的输出。

对于形形色色的NLP任务，OpenAI 的论文列出了一些列输入变换方法，可以处理不同任务类型的输入。下面这张图片来源于论文，展示了处理不同任务的模型结构和对应输入变换。

6.相关问题

Transformer 为什么需要进行 Multi-head Attention？

原论文中说到进行 Multi-head Attention 的原因是将模型分为多个头，形成多个子空间，可以让模型去关注不同方面的信息，最后再将各个方面的信息综合起来。其实直观上也可以想到，如果自己设计这样的一个模型，必然也不会只做一次 attention，多次 attention 综合的结果至少能够起到增强模型的作用，也可以类比 CNN 中同时使用多个卷积核的作用，直观上讲，多头的注意力有助于网络捕捉到更丰富的特征 / 信息。

Transformer 相比于 RNN/LSTM，有什么优势？为什么？

RNN 系列的模型，无法并行计算，因为 T 时刻的计算依赖 T-1 时刻的隐层计算结果，而 T-1 时刻的计算依赖 T-2 时刻的隐层计算结果
Transformer 的特征抽取能力比 RNN 系列的模型要好

为什么说 Transformer 可以代替 seq2seq？

这里用代替这个词略显不妥当，seq2seq 虽已老，但始终还是有其用武之地，seq2seq 最大的问题在于将 Encoder 端的所有信息压缩到一个固定长度的向量中，并将其作为 Decoder 端首个隐藏状态的输入，来预测 Decoder 端第一个单词 (token) 的隐藏状态。在输入序列比较长的时候，这样做显然会损失 Encoder 端的很多信息，而且这样一股脑的把该固定向量送入 Decoder 端，Decoder 端不能够关注到其想要关注的信息。Transformer 不但对 seq2seq 模型这两点缺点有了实质性的改进 (多头交互式 attention 模块)，而且还引入了 self-attention 模块，让源序列和目标序列首先 “自关联” 起来，这样的话，源序列和目标序列自身的 embedding 表示所蕴含的信息更加丰富，而且后续的 FFN 层也增强了模型的表达能力，并且 Transformer 并行计算的能力远远超过了 seq2seq 系列模型

Transformer中的softmax计算为什么需要除以$d_k$?

论文中解释是：向量的点积结果会很大，将softmax函数push到梯度很小的区域，scaled会缓解这种现象。

1.为什么比较大的输入会使得softmax的梯度变得很小

对于一个输入向量$X\subseteq \mathbb{R}^d$ ，softmax函数将其映射/归一化到一个分布 $\hat y\subseteq \mathbb{R}^d$ 。在这个过程中，softmax先用一个自然底数 $e$ 将输入中的元素间差距先“拉大”，然后归一化为一个分布。假设某个输入$X$中最大的的元素下标是$k$ ，如果输入的数量级变大（每个元素都很大），那么$\hat y_k$会非常接近1。

我们可以用一个小例子来看看$X$的数量级对输入最大元素对应的预测概率的$\hat y_k$影响。假定输入$X=[a,a,2a]^T$ ），我们来看不同量级的 $a$产生的$\hat y_3$有什么区别。

a=1时，$\hat y_3$=0.5761168847658291
a=10时，$\hat y_3$=0.999909208384341
a=100时，$\hat y_3 \approx$1.0 (计算机精度限制)

我们不妨把 a 在不同取值下，$\hat y_3$对应的的全部绘制出来。代码如下：

from math import exp
from matplotlib import pyplot as plt
import numpy as np 
f = lambda x: exp(x * 2) / (exp(x) + exp(x) + exp(x * 2))
x = np.linspace(0, 100, 100)
y_3 = [f(x_i) for x_i in x]
plt.plot(x, y_3)
plt.show()

得到的图如下所示：

可以看到，数量级对softmax得到的分布影响非常大。在数量级较大时，softmax将几乎全部的概率分布都分配给了最大值对应的标签。

然后我们来看softmax的梯度。不妨简记softmax函数为 $g(·)$，softmax得到的分布向量$\hat y=g(X)$对输入X的梯度为：

$\frac {\part g(x)}{\part x}=diag(\hat y)-\hat y \hat y^T \in \mathbb{R}^{d \times d}$

把这个矩阵展开：

根据前面的讨论，当输入$X$的元素均较大时，softmax会把大部分概率分布分配给最大的元素，假设我们的输入数量级很大，最大的元素是$x_1$，那么就将产生一个接近one-hot的向量 $\hat y \approx [1,0,···,0]^T$,此时上面的矩阵变为如下形式：

也就是说，在输入的数量级很大时，梯度消失为0，造成参数更新困难。

2.维度与点积大小的关系是怎样的，为什么使用维度的根号来放缩？

针对为什么维度会影响点积的大小，在论文的脚注中其实给出了一点解释：

假设向量$q$和$k$的各个分量是互相独立的随机变量，均值是0，方差是1，那么点积$q \cdot k$均值是0，方差是 $d_k$。

将方差控制为1，也就有效地控制了前面提到的梯度消失的问题。

3.为什么在普通形式的 attention 时，使用非 scaled 的 softmax？

最基础的 attention 有两种形式，一种是 Add [1]，一种是 Mul [2]，写成公式的话是这样：

<> 代表矩阵点积。至于为什么要用 Mul 来完成 Self-attention，作者的说法是为了计算更快。因为虽然矩阵加法的计算更简单，但是 Add 形式套着$tanh$和$v$，相当于一个完整的隐层。在整体计算复杂度上两者接近，但是矩阵乘法已经有了非常成熟的加速实现。在 $d_k$ （即 attention-dim）较小的时候，两者的效果接近。但是随着$d_k$ 增大，Add 开始显著超越 Mul。

作者分析 Mul 性能不佳的原因，认为是极大的点积值将整个 softmax 推向梯度平缓区，使得收敛困难。也就是出现了“梯度消失”。这才有了 scaled。所以，Add 是天然地不需要 scaled，Mul在d_k 较大的时候必须要做 scaled。个人认为，Add 中的矩阵乘法，和 Mul 中的矩阵乘法不同。前者中只有随机变量 X 和参数矩阵 W 相乘，但是后者中包含随机变量 X 和随机变量 X 之间的乘法。

那么，极大的点积值是从哪里来的呢？对于 Mul 来说，如果 $s$ 和 $h$ 都分布在 [0,1]，在相乘时引入一次对所有位置的 $\sum$ 求和，整体的分布就会扩大到 $[0,d_k]$ 。反过来看 Add，右侧是被 $tanh()$ 钳位后的值，分布在 [-1,1]。整体分布和 $d_k$ 没有关系。

4.为什么在分类层（最后一层），使用非 scaled 的 softmax？

同上面一部分，分类层的 softmax 也没有两个随机变量相乘的情况。此外，这一层的 softmax 通常和交叉熵联合求导，在某个目标类别 $i$ 上的整体梯度变为$y_i^{‘}-y_i$ ，即预测值和真值的差。当出现某个极大的元素值，softmax 的输出概率会集中在该类别上。如果是预测正确，整体梯度接近于 0，抑制参数更新；如果是错误类别，则整体梯度接近于1，给出最大程度的负反馈。

也就是说，这个时候的梯度形式改变，不会出现极大值导致梯度消失的情况了。

该问题详细回答可以看这篇知乎问题

Transformer详解