由二叉树的定义可知，一棵二叉树由根结点、左子树和右子树三部分组成。因此，只要遍历了这三个部分，就可以实现遍历整个二叉树。若以D、L、R分别表示遍历根结点、左子树、右子树，则二叉树的递归遍历可以有一下四种方式：

1
2
3
4
5
6
7
/* 二叉树遍历框架 */
def traverse(TreeNode root):
    // 前序遍历
    traverse(root.left)
    // 中序遍历
    traverse(root.right)
    // 后序遍历

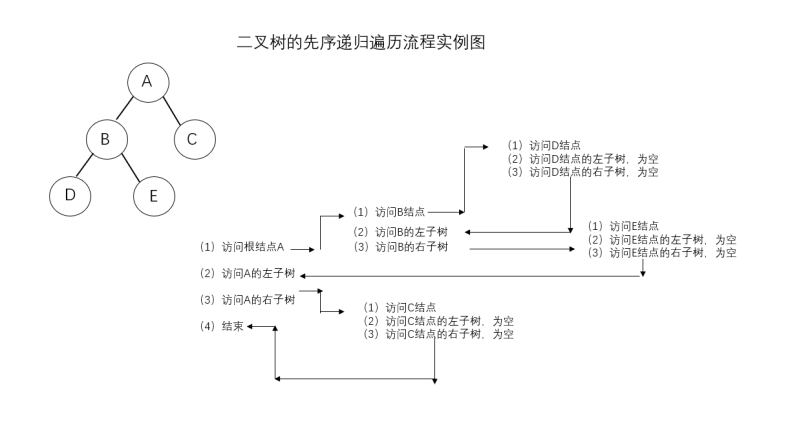
1、先序遍历（DLR）

口诀：根左右。前序遍历首先访问根结点然后遍历左子树，最后遍历右子树。在遍历左、右子树时，仍然先访问根节点，然后遍历左子树，最后遍历右子树。
若二叉树为空则结束返回，否则：
（1）访问根结点。
（2）前序遍历左子树。
（3）前序遍历右子树 。
需要注意的是：遍历左右子树时仍然采用前序遍历方法。

举例：

img

先序遍历结果：ABDEC

注意：已知后序遍历和中序遍历，就能确定先序遍历。

代码：先序遍历：根节点->左子树->右子树

1
2
3
4
5
6
7
# 前序打印二叉树（递归）
def preOrderTraverse(node):
     if node is None:
         return None
     print(node.val)
     preOrderTraverse(node.left)
     preOrderTraverse(node.right)

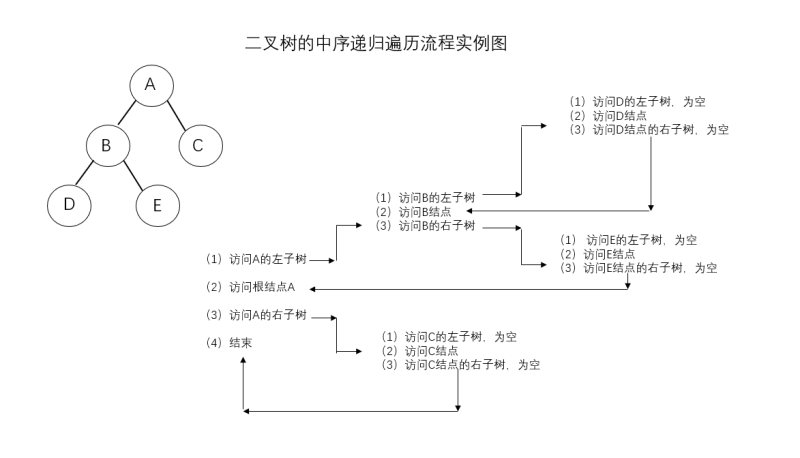
2、中序遍历（LDR）

口诀：左根右。中序遍历首先遍历左子树，然后访问根结点，最后遍历右子树。

举例：

img

中序遍历结果：DBEAC

注：二叉搜索树题目一般和中序遍历相关。

代码：中序遍历：左子树->根节点->右子树

1
2
3
4
5
6
7
# 中序打印二叉树（递归）
def inOrderTraverse(node):
     if node is None:
         return None
     inOrderTraverse(node.left)
     print(node.val)
     inOrderTraverse(node.right)

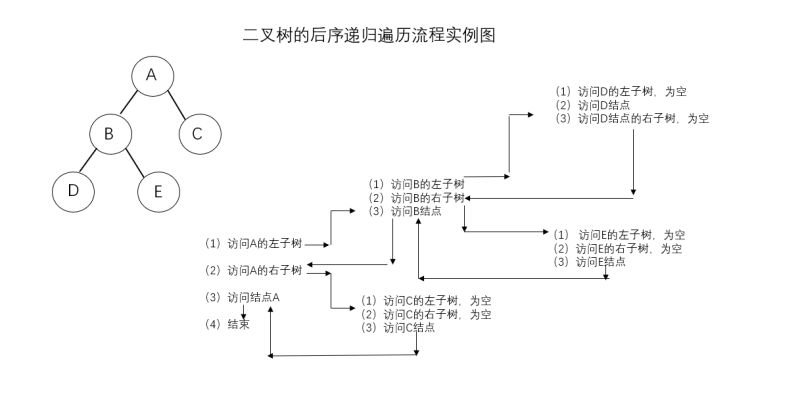
3、后序遍历（LRD）

口诀：左右根。后序遍历首先遍历左子树，然后遍历右子树，最后访问根结点，在遍历左、右子树时，仍然先遍历左子树，然后遍历右子树，最后遍历根结点。即：
若二叉树为空则结束返回，
否则：
（1）后序遍历左子树
（2）后序遍历右子树
（3）访问根结点

举例：

img

后序遍历结果：DEBCA

注：已知前序遍历和中序遍历，就能确定后序遍历。

代码：后序遍历：左子树->右子树->根节点

1
2
3
4
5
6
7
# 后序打印二叉树（递归）
def postOrderTraverse(node):
     if node is None:
         return None
     postOrderTraverse(node.left)
     postOrderTraverse(node.right)
     print(node.val)

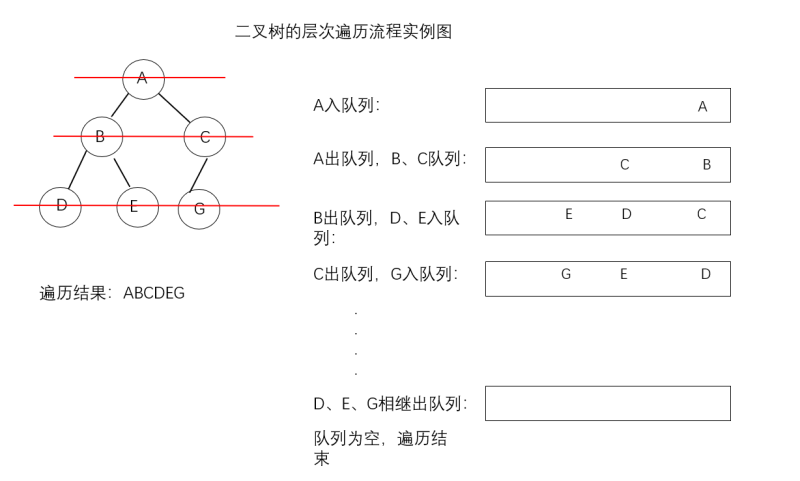
4、层次遍历

（1）根结点入队列

（2）根结点出队列，根结点的左子树、右子树相继入队列

（3）根结点的左子树结点出队列，左子树结点的左子树、右子树相继入队列

（4）…….

举例：

img

层次遍历结果：ABCDEG

代码：按层遍历：从上到下、从左到右按层遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# 先进先出选用队列结构
  import queue
  def layerTraverse(head):
      if not head:
          return None
      que = queue.Queue()      # 创建先进先出队列
      que.put(head)
      while not que.empty():
          head = que.get()    # 弹出第一个元素并打印
          print(head.val)
          if head.left:       # 若该节点存在左子节点,则加入队列（先push左节点）
              que.put(head.left)
          if head.right:      # 若该节点存在右子节点,则加入队列（再push右节点）
              que.put(head.right)